Given that most people have never come into contact with a Night Vision Device (NVD), people who are familiar with the sound of one powering up have likely heard it in action movies or video games, particularly those in the Tom Clancy's Splinter Cell series. Sadly, modern NVDs no longer make that distinctive noise, but the sound continues to live on in popular media.

It's a sound that's actually very similar to an old fashioned camera flash charging up: one of it's main features being a high frequency whine increasing linearly over the course of a second or two.

To figure out exactly what's going on, it's useful to perform some spectral analysis. The spectrogram for the sound above is as follows:

At the very start, it's not exactly crystal clear what's happening, but we can see that, fundamentally speaking, the sound starts quite high at around 5000 Hz, very rapidly decreases to about 1500 Hz, then gradually climbs back up to 2500 Hz.

As for the waveform itself, we can use a frequency analyser to visualise its harmonic content. We discover that the sound is quite a simple one, consisting of 6 prominent harmonics, which will be quite straightforward to recreate in Web Audio, as explained a little later on.

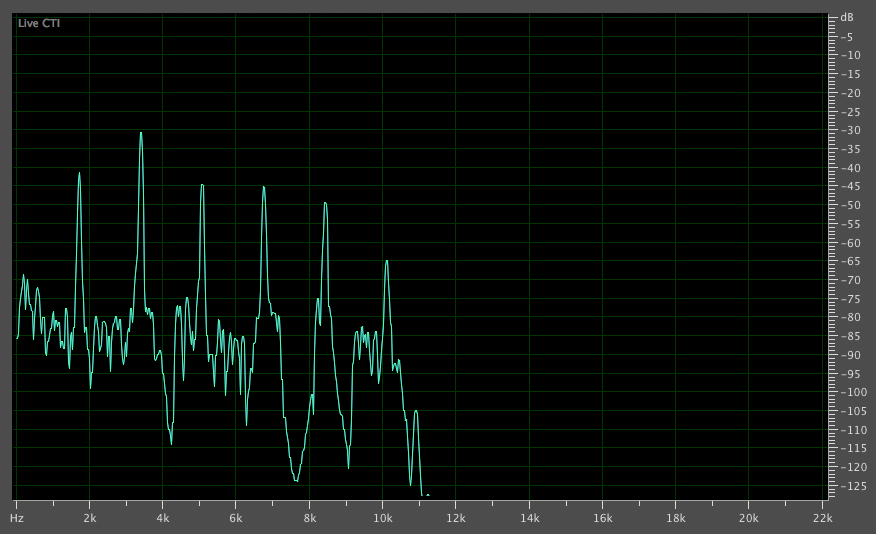
We now have all the information needed to recreate this with Web Audio. First, as ever, we create the Audio Context.

var context = new AudioContext();

As in previous tutorials, we'll create an object, NVD(), to hold all our properties and methods. We'll also take the opportunity to create our gain node and connect it to the speakers.

function NVD(context){
	this.context = context; // the audio context
	this.downSweepTime = 0.04; // the time taken for the initial sweep 
	this.upSweepTime = 1.525; // the time taken for the second sweep 
	this.initialFrequency = 5000;
	this.lowestFrequency = 1500;
	this.finalFrequency = 2500;
	this.maxGainValue = 0.2;

	this.gainNode = context.createGain();
	this.gainNode.connect(this.context.destination);
}

To trigger our sound, we need to create a play function. The first thing we need to do in this function is create an oscillator node and connect it to our gainNode. Then we need to start the oscillator and schedule the changes in frequency we outlined earlier using Web Audio's ramp functions.

These ramp functions take two inputs: the first is the value you want your parameter to end up with, and the second is the time at which you want it to reach this value. The ramp starts from the time you last explicitly set a value, which is why we need the line this.osc.frequency.setValueAtTime(5000, time). Given that time will be the moment we start our oscillator, our ramp will start from that moment too.

During the second sweep, we'll also use linearRampToVAlueAtTime on the gainNode to gradually fade our gain to zero, creating a more polished effect.

NVD.prototype.play = function(time){
	this.osc = context.createOscillator();
	this.osc.connect(this.gainNode);

	this.osc.start(time)
	this.osc.frequency.setValueAtTime(this.initialFrequency, time);
	this.osc.frequency.linearRampToValueAtTime(this.lowestFrequency, time + this.downSweepTime); 
	this.osc.frequency.linearRampToValueAtTime(this.finalFrequency, time + this.downSweepTime + this.upSweepTime);

	this.gainNode.gain.setValueAtTime(this.maxGainValue, time);
	this.gainNode.gain.linearRampToValueAtTime(0, time + this.downSweepTime + this.upSweepTime);

	this.osc.stop(time + this.downSweepTime + this.upSweepTime);
}

If you tried playing this, it would sound pretty close to the finished thing, but the timbre is not right. That's because our oscillator is still using its default sine shaped waveform - we need to apply a custom waveform which we learned about from the spectral analysis we performed earlier. We'll create a new method called setOscillatorWaveform() which will be called from within the play method.

NVD.prototype.setOscillatorWaveform = function(){

	// We're omitting the final harmonic because it's so faint compared to the others it's negligible
	var coeffs = [
		0, 
		0.010, 
		0.022,
		0.007,
		0.004,
		0.004
	];
	var real = new Float32Array(coeffs);	
	var imag = new Float32Array(real.length); // creates an array of zeros.
	var wave = context.createPeriodicWave(real, imag);
	this.osc.setPeriodicWave(wave);
}

The createPeriodicWave function takes two inputs: an array of real (cosine) terms, and an array of imaginary (sine) terms. The browser performs an inverse Fourier transform to get a time domain buffer for the particular frequency of the oscillator.

Our coeffs arary contains the intensities of each harmonic, which we calculated earlier on. Note that the first element in the array corresponds to a DC (direct current) offset, and because this is not relevant in our scenario, we set it to zero. The second element corresponds to the fundamental frequency, the third element corresponds to the first overtone (twice the value of the fundamental), and so on and so forth. Also, in this particular case, we do not need to provide any sine terms so that array is populated with zeros.

Our graph showed these values in deciBels, but we converted them to intensities with the formula: coeff = Math.pow(10,(coeff_in_dB/20));

That essentially completes all the hard work required, and all that remains is to create a simple user interface to trigger the sound.

<button id='js-trigger-sound'>Click for night vision sound</button>

<script>
// create the audio context
var context = new AudioContext();

$("#js-trigger-sound").click(function(e){
	e.preventDefault();
	// Create an NVD instace.
	var nvd = new NVD(context);
	nvd.play(context.currentTime);
});
</script>

See the Pen Night Vision Goggles Sound by Ed Ball (@edball) on CodePen.

Header image: AN/PVS-14 Monocular Night Vision Device (MNVD) by Program Executive Office Soldier